Introduction to Reinforcement Learning: Concepts and Algorithms

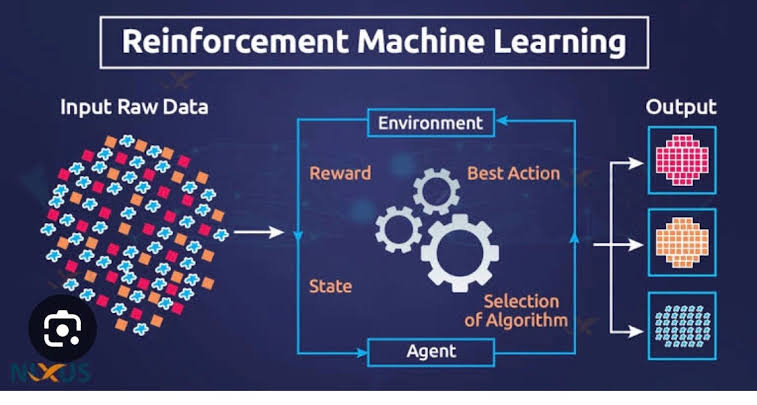
Reinforcement Learning (RL) is a subset of machine learning where an agent learns to make decisions by interacting with an environment. The agent learns to achieve a goal by taking actions and receiving feedback in the form of rewards or punishments. This trial-and-error learning process is inspired by the way humans and animals learn from their experiences. In this article, we will explore the fundamental concepts of reinforcement learning, delve into the core algorithms, and discuss their applications.

Understanding Reinforcement Learning

In reinforcement learning, the agent interacts with an environment through actions. The environment provides feedback in the form of rewards or punishments based on the actions taken. The agent's goal is to learn a policy—a strategy for choosing actions—that maximizes the cumulative reward over time.

The key components of reinforcement learning are:

- Agent: The entity that makes decisions and learns from interactions.

- Environment: The external system with which the agent interacts.

- State: A representation of the current situation of the environment.

- Action: A decision or move made by the agent.

- Reward: Feedback from the environment based on the action taken.

- Policy: A strategy used by the agent to determine actions based on states.

- Value Function: A function that estimates the expected cumulative reward of states or state-action pairs.

Markov Decision Processes

Reinforcement learning problems are often modeled using Markov Decision Processes (MDPs). An MDP provides a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. An MDP is defined by:

- A set of states (S) representing all possible situations in the environment.

- A set of actions (A) available to the agent.

- A transition function (P) that defines the probability of moving from one state to another given a specific action.

- A reward function (R) that provides the immediate reward received after transitioning from one state to another due to an action.

- A discount factor (γ) that determines the importance of future rewards.

The goal in an MDP is to find an optimal policy that maximizes the expected cumulative reward, often referred to as the return.

Key Concepts in Reinforcement Learning

Several key concepts underpin reinforcement learning, enabling agents to learn optimal policies.

Exploration vs. Exploitation

A fundamental challenge in reinforcement learning is balancing exploration (trying new actions to discover their effects) and exploitation (choosing actions that maximize reward based on current knowledge). Effective learning requires a balance between exploring the environment to gain more information and exploiting known information to maximize rewards.

Value Functions

Value functions estimate the expected cumulative reward of states or state-action pairs. Two important value functions in reinforcement learning are:

- State-Value Function (V): Represents the expected cumulative reward of a state under a policy.

- Action-Value Function (Q): Represents the expected cumulative reward of a state-action pair under a policy.

Bellman Equations

The Bellman equations provide a recursive relationship for value functions. They express the value of a state or state-action pair in terms of the immediate reward and the value of the subsequent state. The Bellman equations form the foundation for many reinforcement learning algorithms.

Core Reinforcement Learning Algorithms

Several key algorithms are fundamental to reinforcement learning. These algorithms can be broadly categorized into value-based methods, policy-based methods, and model-based methods.

Value-Based Methods

Value-based methods focus on estimating value functions and deriving policies from them. The most well-known value-based algorithm is Q-learning.

Q-Learning

Q-learning is an off-policy algorithm that aims to learn the optimal action-value function (Q*). The agent updates the Q-values using the Bellman equation:

Q(s, a) = Q(s, a) + α [r + γ max(Q(s', a')) - Q(s, a)]

where:

- Q(s, a) is the current Q-value of state-action pair (s, a).

- α is the learning rate.

- r is the reward received after taking action a in state s.

- γ is the discount factor.

- max(Q(s', a')) is the maximum Q-value of the next state-action pair (s', a').

The agent selects actions based on an ε-greedy policy, where it chooses the action with the highest Q-value most of the time but occasionally explores random actions.

Policy-Based Methods

Policy-based methods focus directly on optimizing the policy without explicitly estimating value functions. These methods are particularly useful for high-dimensional or continuous action spaces. One popular policy-based algorithm is the REINFORCE algorithm.

REINFORCE Algorithm

The REINFORCE algorithm is a Monte Carlo policy gradient method. It optimizes the policy by adjusting its parameters in the direction that maximizes the expected cumulative reward. The policy parameters are updated using the following gradient ascent rule:

θ = θ + α ∇_θ log πθ(s, a) R

where:

- θ represents the policy parameters.

- α is the learning rate.

- πθ(s, a) is the policy.

- R is the cumulative reward.

The REINFORCE algorithm is simple but suffers from high variance in the gradient estimates.

Actor-Critic Methods

Actor-critic methods combine value-based and policy-based approaches. They use two components: an actor, which updates the policy, and a critic, which estimates the value function. The actor adjusts the policy parameters in the direction suggested by the critic. This combination reduces the variance in policy updates.

Model-Based Methods

Model-based methods involve learning a model of the environment's dynamics and using this model to plan and make decisions. These methods are more sample-efficient but require accurate modeling of the environment. One example of a model-based method is the Dyna-Q algorithm.

Dyna-Q Algorithm

The Dyna-Q algorithm integrates model-based planning with Q-learning. It uses real experiences to update the Q-values and simultaneously learns a model of the environment. The learned model is then used to simulate additional experiences, further updating the Q-values. This approach accelerates learning by leveraging both real and simulated experiences.

Applications of Reinforcement Learning

Reinforcement learning has numerous applications across various domains:

- **Game Playing**: RL has been successfully applied to games like Chess, Go, and video games. AlphaGo, developed by DeepMind, famously defeated world champions in Go using RL.

- **Robotics**: RL is used in robotics for tasks such as navigation, manipulation, and control. Robots learn to perform complex actions through trial and error.

- **Autonomous Vehicles**: RL is employed in autonomous driving for decision-making and control. Self-driving cars learn to navigate and make safe driving decisions.

- **Healthcare**: RL is applied in healthcare for personalized treatment planning, drug discovery, and robotic-assisted surgery. It helps optimize treatment strategies and improve patient outcomes.

- **Finance**: RL is used in algorithmic trading, portfolio management, and fraud detection. It helps optimize investment strategies and identify anomalies.

Conclusion

Reinforcement learning is a powerful paradigm that enables agents to learn from interactions with their environment. By balancing exploration and exploitation, estimating value functions, and optimizing policies, RL algorithms achieve remarkable performance in various applications. Understanding the core concepts and algorithms of reinforcement learning provides a foundation for leveraging its potential in solving complex real-world problems. As research and development in RL continue to advance, we can expect even more innovative and impactful applications in the future.