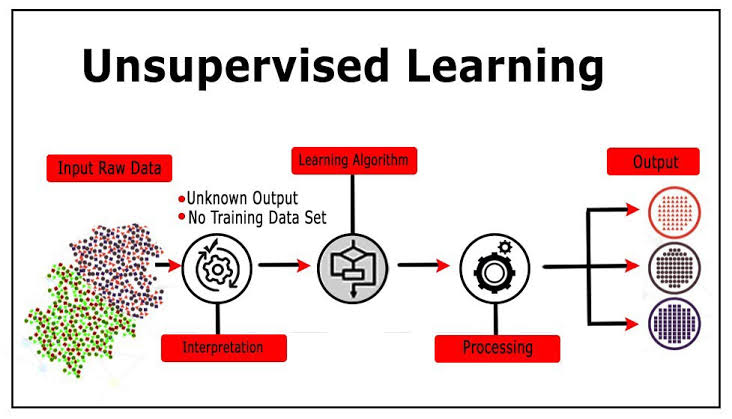
Unsupervised learning is type of machine learning where model learns patterns from unlabelled data without predefined categories or outcomes. This approach is particularly valuable. It helps in exploring and understanding complex data sets. Two critical techniques in unsupervised learning are clustering and dimensionality reduction. These methods help in organizing data into meaningful structures. They reduce the complexity of data. This uncover hidden patterns. This comprehensive examination delves into these techniques. Also their applications and their significance in data analysis.
Clustering is technique used to group similar data points into clusters based on their features. The goal is to identify inherent groupings within data. This allows for more structured analysis. Several clustering methods are commonly used. Each with its strengths and applications
K-means clustering is one of the most widely used clustering algorithms. It partitions data into K distinct clusters. Each data point belongs to the cluster with the nearest mean. The process involves initializing K centroids. Then assigning each data point to the nearest centroid and updating the centroids based on assigned points. This iterative process continues until centroids stabilize. K-means is favored for simplicity and efficiency but it requires specifying number of clusters beforehand. This can be challenging if optimal number is unknown.
Hierarchical Clustering
Hierarchical clustering creates a tree-like structure of clusters, which can be visualized as a dendrogram. There are two main types: agglomerative and divisive. Agglomerative hierarchical clustering starts with each data point as its own cluster and iteratively merges the closest clusters. In contrast, divisive hierarchical clustering begins with a single cluster and recursively splits it. Hierarchical clustering does not require specifying the number of clusters in advance and provides a comprehensive view of data structure. However, it can be computationally intensive and may not scale well with very large datasets.
DBSCAN (Density-Based Spatial Clustering of Applications with Noise)
DBSCAN is a density-based clustering method that groups data points based on their density. Unlike K-means, which assumes spherical clusters, DBSCAN can identify clusters of arbitrary shapes and sizes. It operates by defining a neighborhood around each point and expanding clusters based on the density of points within these neighborhoods. Points that do not meet the density criteria are considered noise. DBSCAN is effective in discovering clusters with varying shapes and sizes, but its performance can be sensitive to the choice of parameters, such as the neighborhood radius.
Dimensionality Reduction Techniques
Dimensionality reduction involves reducing the number of features in a dataset while preserving its essential structure. This technique simplifies data, making it easier to visualize and analyze. It is particularly useful when dealing with high-dimensional data, where traditional methods may struggle.
Principal Component Analysis (PCA)
Principal Component Analysis (PCA) is a statistical technique that transforms high-dimensional data into a lower-dimensional form by identifying the directions (principal components) in which the data varies the most. PCA projects the data onto a new set of axes, ordered by the amount of variance captured. The first few principal components often capture the majority of the variance, allowing for dimensionality reduction. PCA is widely used in exploratory data analysis and feature reduction but may struggle with non-linear relationships between features.
t-Distributed Stochastic Neighbor Embedding (t-SNE)
t-Distributed Stochastic Neighbor Embedding (t-SNE) is a non-linear dimensionality reduction technique that excels in preserving local structures within data. It works by converting similarities between data points into probabilities and then minimizing the divergence between these probabilities in the lower-dimensional space. t-SNE is particularly effective for visualizing complex, high-dimensional data, such as images or genetic data. However, it can be computationally expensive and may not scale well with very large datasets.
Autoencoders
Autoencoders are neural network-based models designed for unsupervised dimensionality reduction. They consist of an encoder, which compresses the input data into a lower-dimensional representation, and a decoder, which reconstructs the original data from this representation. Autoencoders learn to encode the data in a way that preserves its essential features while reducing its dimensionality. They are highly flexible and can be adapted to various types of data, but they require careful tuning and can be complex to train.
Applications and Significance
Unsupervised learning techniques, particularly clustering and dimensionality reduction, have a wide range of applications across various domains.
Market Segmentation
In business and marketing, clustering techniques can be used to segment customers based on purchasing behavior, demographics, or preferences. This segmentation allows companies to tailor their strategies and offerings to different customer groups, enhancing marketing effectiveness and customer satisfaction.
Image and Video Analysis
In computer vision, dimensionality reduction methods like PCA and autoencoders are used to compress and analyze high-dimensional image and video data. This compression can lead to faster processing times and improved performance in tasks such as object recognition and classification.
Genomics and Bioinformatics
In genomics, clustering techniques are employed to group genes or proteins with similar expression patterns, aiding in the discovery of gene functions and interactions. Dimensionality reduction methods help in visualizing and interpreting complex biological data, such as gene expression profiles.
Anomaly Detection
Clustering and dimensionality reduction can be applied to anomaly detection, identifying unusual patterns or outliers in data. For example, in network security, these techniques can help detect fraudulent activities or intrusions by analyzing network traffic patterns.
Conclusion
Unsupervised learning techniques, including clustering and dimensionality reduction, play a vital role in understanding and analyzing complex data. By organizing data into meaningful structures and reducing its dimensionality, these methods enable more insightful analyses and practical applications across various fields. As data continues to grow in complexity, the importance of these techniques in uncovering hidden patterns and facilitating decision-making will only increase.